In addition to their increased accuracy and robustness, high-order methods can lead to better utilization of modern multi-core and heterogeneous computer architectures. We demonstrate this by combining several layers of parallelism in the software implementation of our numerical algorithms:
- MPI-based parallel finite elements in MFEM (domain-decomposed between CPUs)
- CUDA-based parallel kernels in BLAST (zone-decomposed on GPUs)
- OpenMP-based parallel kernels in BLAST (data-decomposed between CPU cores)
In particular, our hybrid MPI+CUDA+OpenMP high-order algorithms can take full advantage of parallel clusters with multi-core processors and GPU accelerators on each node.
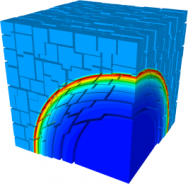
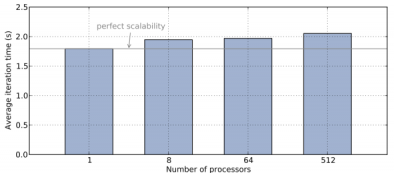
Parallel MPI Weak Scalability of a 3D Sedov Blast Simulation with Q2-Q1 Finite Elements
MPI simulation up to 512 processors with fixed problem size per processor (approximately 512 Q2-Q1 zones). Unstructured parallel domain decomposition and weak scalability are shown below.
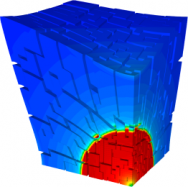
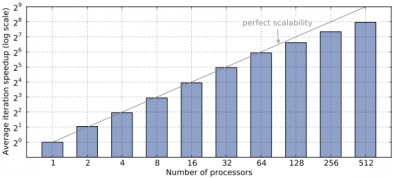
Parallel MPI Strong Scalability of a 3D Noh Implosion Simulation with Q2-Q1 Finite Elements
MPI simulation up to 512 processors with fixed total problem size. Unstructured parallel domain decomposition and strong scalability are shown below. Note that we get good performance on 512 processors with only 64 Q2-Q1 zones per processor.
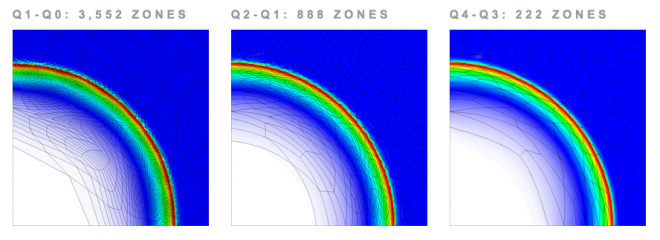
Comparing Hardware Utilization with High-Order Finite Elements for 2Drz Sedov Problem
Parallel simulation on 48 processors (Intel Xeon EP X5660) with fixed number of unknowns, using Q1-Q0, Q2-Q1 and Q4-Q3 finite elements on unstructured 2D mesh. High-order finite element methods have much greater flop/byte ratios in 2D leading to improved hardware utilization.
| Performance metric | Q1-Q0 | Q2-Q1 | Q4-Q3 |
|---|---|---|---|
| no. cycles | 4,799 | 5,017 | 4,660 |
| run time(s) | 10.88 | 11.39 | 15.62 |
| no. qpts/zone | 4 | 16 | 64 |
| no. floating point operations | 1.00e11 | 1.54e11 | 4.75e11 |
| % floating point ops/total instructions | 13.56% | 16.4% | 22.2% |
| Gflops | 9.2 | 13.5 | 30.4 |
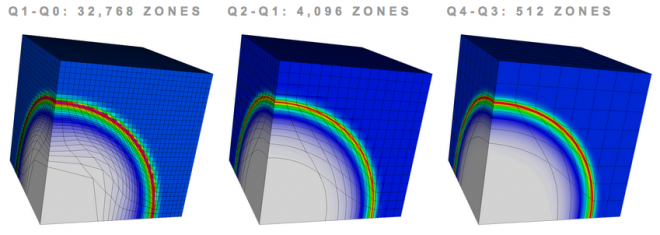
Comparing Hardware Utilization with High-Order Finite Elements for 3D Sedov Problem
Parallel simulation on 256 processors (Intel Xeon E5-2670) with fixed number of unknowns, using Q1-Q0, Q2-Q1 and Q4-Q3 finite elements on 3D mesh. High-order finite element methods have much greater flop/byte ratios in 3D leading to improved hardware utilization.
| Performance metric | Q1-Q0 | Q2-Q1 | Q4-Q3 |
|---|---|---|---|
| no. cycles | 3,273 | 1,017 | 983 |
| run time (s) | 34.90 | 14.43 | 76.95 |
| no. qpts/zone | 8 | 64 | 512 |
| no. floating point operations | 3.82e12 | 2.53e12 | 3.34e13 |
| % floating point ops/total instructions | 19.42% | 22.85% | 26.84% |
| Gflops | 109.5 | 175.3 | 434.1 |
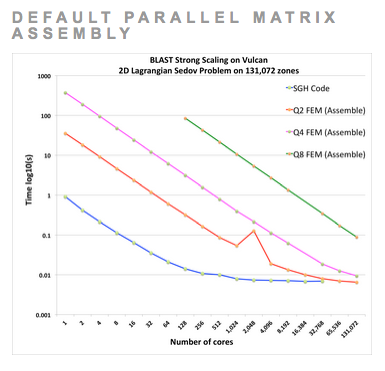
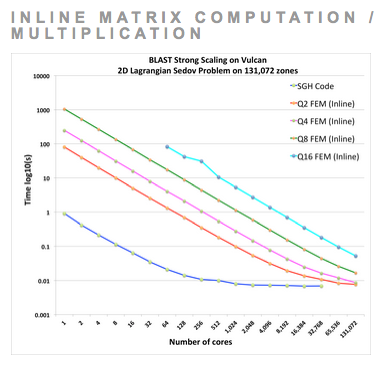
Extreme Parallel MPI Strong Scalability of a 2D Sedov Simulation with Very High-Order Finite Elements
Comparing extreme strong scaling results on 131,072 processors of LLNL's Vulcan computer for the 2D Sedov test problem using two different approaches for high-order parallel finite element computations: our default approach where high-order matrices are assembled and applied globally (left) and a new "action-based" approach where finite element matrices are computed and applied on the fly (right). The "action based" approach favors the very high-order methods (Q4 and beyond) by trading memory usage / bandwidth for inline floating point operations, resulting in a reduced memory foot print and improved run times for very high-order methods. For each case, the mesh size is fixed, leading to increased spatial resolution as the order of the finite elements is increased. High-order finite element methods have much greater flop/byte ratios than traditional low order staggered grid hydro (SGH) methods, leading to better strong parallel scaling, including the ability to strong-scale all the way down to a single computational zone per core.
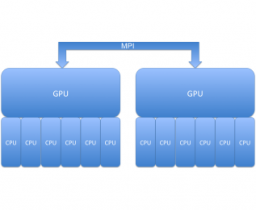
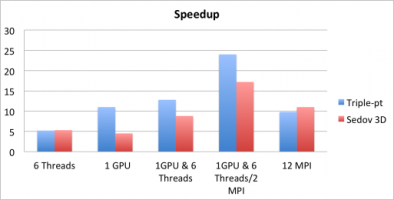
On-n [Inline Matrix Computation / Multiplication] ode MPI/CUDA/OpenMP Scalability
Results from 2D Q3-Q2 triple-point shock interaction and 3D Q2-Q1 Sedov blast simulations on a node of a parallel cluster with two Intel 6 Core Xeon CPUs and two NVIDIA M2050 GPU cards, as shown on the left below. The critical corner force routine in BLAST is parallelized by different methods, compared on the right below. In these settings, one GPU performs similarly to a six-core CPU, and the hybrid MPI+CUDA+OpenMP approach is 2.5x faster compared to full MPI (12 tasks) on the node.
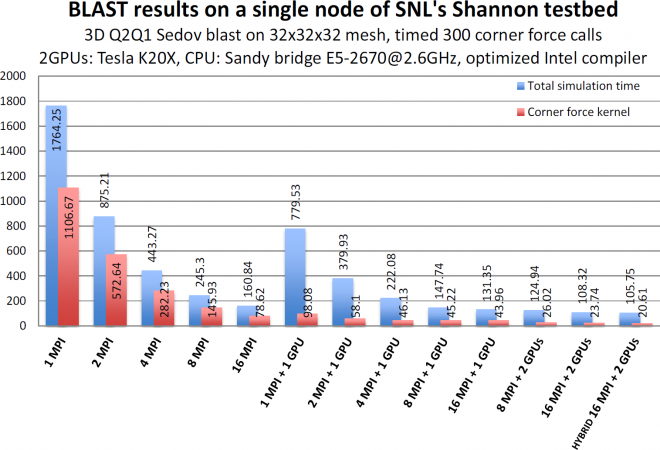
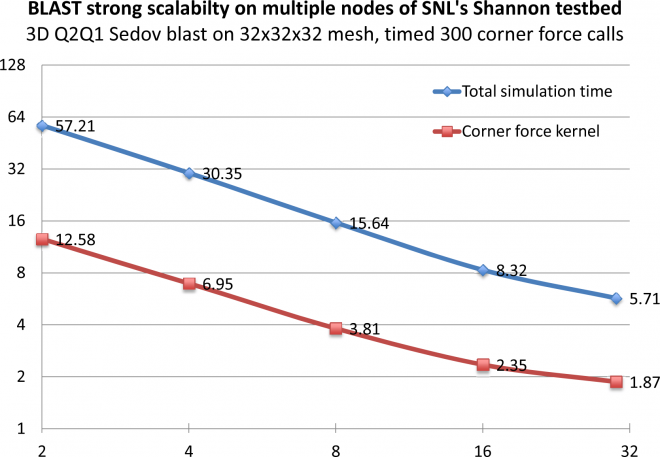
The Hyper-Q technology on the Kepler architecture allows multiple MPI tasks to simultaneously use the same GPU. Results from 3D Q2-Q1 Sedov blast problem run on nodes of SNL's Shannon testbed with a Sandy bridge CPU and 2 Tesla K20X GPUs show significant improvements (up to 4X) in the corner force kernel computation, as well as the overall BLAST simulation time.
Contact: Tzanio Kolev, kolev1@llnl.gov