We consider a simple 1D multi-material problem, which captures key aspects of inertial confinement fusion (ICF) implosion dynamics, on unstructured 2D and 3D meshes. The problem consists of two regions, each with an ideal gas equation of state. Initial conditions and material properties are specified according to the following diagram:
The outer surface drives a spherical shock wave inward. The interface between the high- and low-density materials should remain perfectly spherical for all time due to the spherical symmetry of the velocity drive. However, discretization errors of the initial geometry and subsequent error introduced by the numerical algorithm will be amplified over time since the interface is subject to both Richtmyer-Meshkov (RM) and Rayleigh-Taylor (RT) instabilities. Maintaining spherical symmetry on 2D and 3D unstructured meshes remains a major challenge for most Lagrangian (or ALE) schemes.
2D Axisymmetric Lagrangian Simulations with Q2-Q1 Finite Elements on Unstructured Meshes
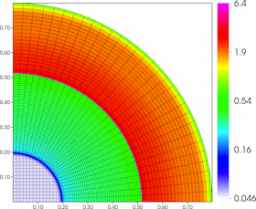
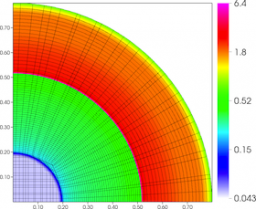
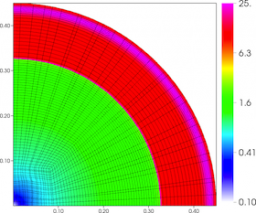
Results for density and curvilinear mesh in the 2D axisymmetric ICF-like problem on a uniform unstructured mesh at times t = 0.0, 0.08 and 0.15.
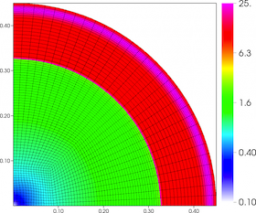
Results for density and curvilinear mesh in the 2D axisymmetric ICF-like problem on a randomized unstructured mesh at times t = 0.0, 0.08 and 0.15.
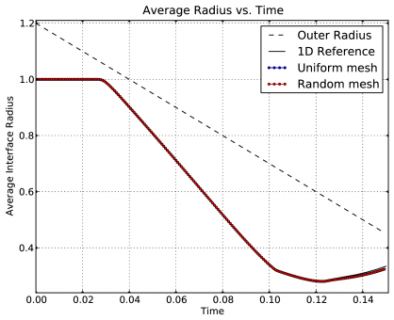
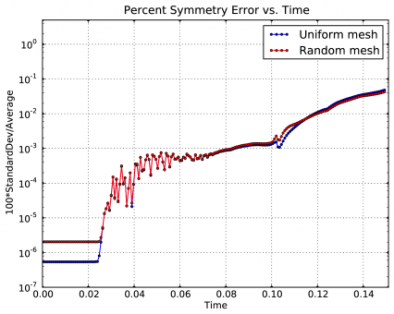
Time dependent results for average interface radius and percent symmetry error for both uniform and random meshes.
We observe a sharp rise in symmetry error as the shock first passes over the interface around t = 0.03 and impulsively accelerates it, due to the RM instability. As the shell begins to decelerate due to multiple shock reflections from the origin around t = 0.11, the interface is subject to RT instability and we observe another sharp increase in symmetry error. Nevertheless, the final symmetry error is less than 0.1% in both cases. High-order Lagrangian methods excel at symmetry preservation on non-uniform and unstructured meshes.
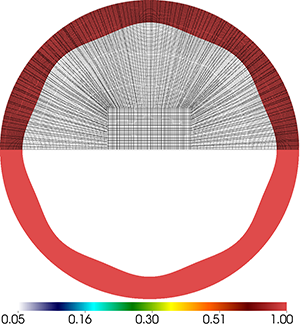
3D Lagrangian Simulations with Q1-Q0, Q2-Q1 and Q4-Q3 Finite Elements on an Unstructured Mesh
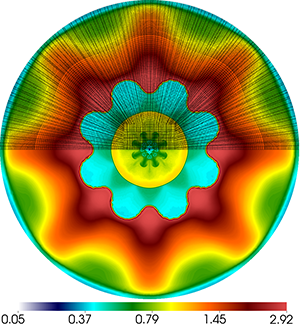
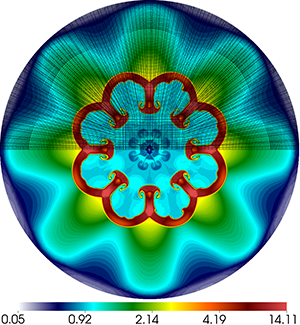
Results for density and curvilinear mesh in the 3D ICF-like problem on an unstructured mesh using Q1-Q0, Q2-Q1 and Q4-Q3 finite elements (top to bottom) at times t = 0.0, 0.08 and 0.15. The three calculations have the same number of kinematic degrees of freedom.
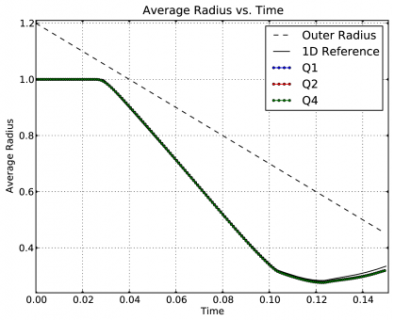
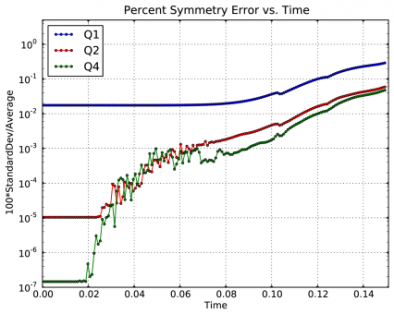
Time dependent results for average interface radius and percent symmetry error for the Q1-Q0, Q2-Q1 and Q4-Q3 cases.
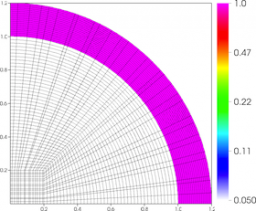
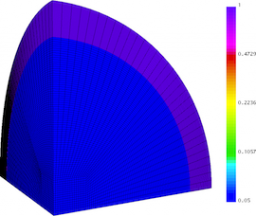
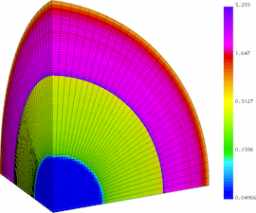
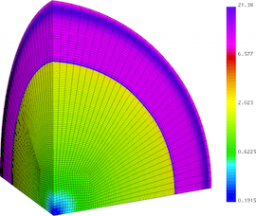
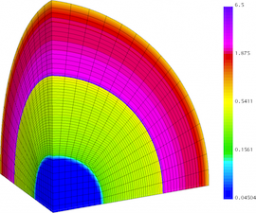
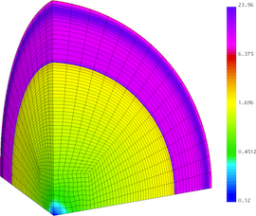
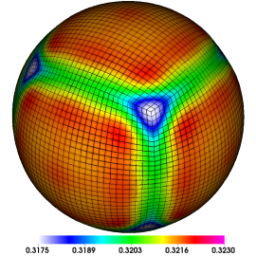
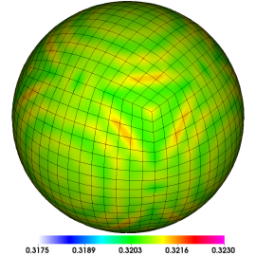
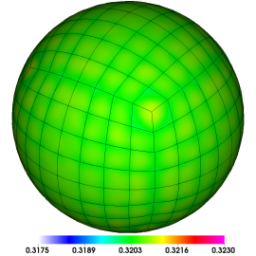
Spherical surface plots of interface radius using a fixed color scale at the final time for the Q1-Q0, Q2-Q1 and Q4-Q3 cases. High-order Lagrangian methods excel at symmetry preservation on 3D unstructured meshes.
2D Planar Perturbed ALE Simulations with Q4-Q3 Finite Elements on Unstructured Meshes
2D perturbed ICF simulation results on unstructured uniform grid High-order ALE methods excel at minimizing mesh imprinting on non-uniform and unstructured meshes.
Multi-material Cylindrical ALE Simulation
2D perturbed ICF simulation results on unstructured grid with two materials and second order finite element method at different time instances (click for larger view).
Contact: Tzanio Kolev, kolev1@llnl.gov