Overview
The fundamental equation governing a non-relativistic quantum system of N particles is the time-dependent Schroedinger Equation [Schroedinger, 1926]. In 1965, Kohn and Sham proposed to replace this original many-body problem by an auxiliary independent-particles problem that can be solved more easily, and formulated the equations of Density Functional Theory (DFT).
Solving this simplified problem requires to find the subspace of dimension N spanned by the N eigenfunctions Ψi corresponding to the N lowest eigenvalues εi of a non-linear Hamiltonian operator H determined from first-principles. From the solution of the Kohn-Sham equations, forces acting on atoms can be derived to optimize geometries and simulate finite temperature phenomenon by (First-Principles) molecular dynamics.
Application examples
First-Principles molecular dynamics is used in various areas at LLNL such as
- Studying chemical reactions in molecular biology
- Predicting and characterizing structural, electronic and dynamical properties of materials under extreme conditions
- Model interfaces such as
- water-semiconductor interfaces in order to understand the microscopic mechanisms involved in photocatalytic water splitting
- electrode-electrolyte in batteries and capacitors to improve design of electrolyte/anode systems and identify the specific factors that control their performance
O(N3) complexity problem in Density Functional Theory
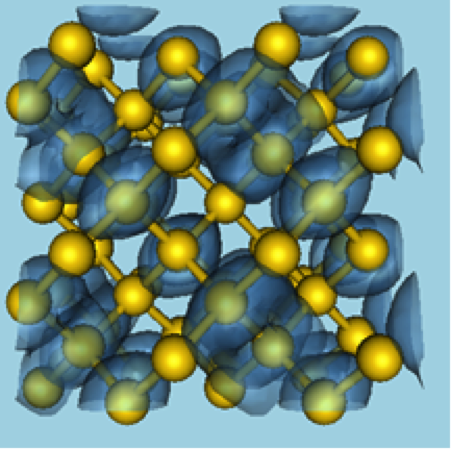
- Standard computational algorithms represent the electrons by N quantum wave functions extended over the whole computational domain (see Fig. 1)
- This leads to O(N2) storage requirements and O(N3) arithmetic operations
- Using LLNL powerful super-computers, relatively large problems can be solved (~1000 atoms). But this O(N3) complexity becomes a critical bottleneck which limits our computational capabilities to study larger and more realistic physical systems, for instance materials with realistic defects and/or realistic concentrations of alloying species
Maximally localized Wannier functions representation
- The electronic structure can be represented by a set of "localized" orbitals with a limited spread independent of the system size ("Maximally Localized Wannier Functions")
- These functions can be obtained from the eigenfunctions of the Hamiltonian operator by an orthogonal transformation (see Fig. 2)
- This transformation is still an O(N3) complexity operation, but it shows that a more compact/sparse representation of the electronic structure is possible
O(N) complexity algorithm
The O(N) complexity algorithm for First-Principles molecular dynamics we are developing is based on the following ideas:
- Formulate the equations of DFT in terms of general non-orthogonal orbitals (instead of eigenfunctions)
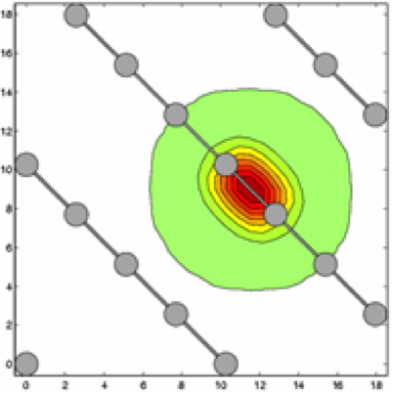
- Represent the occupied electronic orbitals on real-space uniform mesh, using a finite difference discretization
- Compute directly localized orbitals (truncated beyond a cutoff radius) by minimizing an energy functional with localization constraints that only marginally affect accuracy (Figure 3 and 4)
- Compute approximately the selected elements of the inverse of the sparse Gram (overlap) matrix that enter the equations of DFT for non-orthogonal orbitals, by inverting principal submatrices of the global Gram matrix (see references [6] and [7])
Overcoming the cubic scaling wall
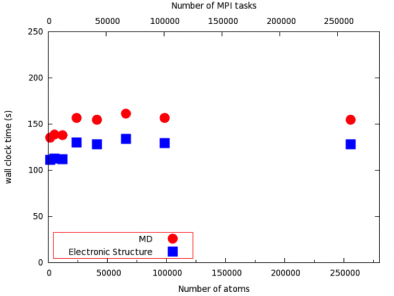
For molecular systems with a band gap, we have demonstrated that this "localized orbitals" technique becomes more efficient than the traditional Plane Waves approach for physical systems larger than ~500 atoms. We have also demonstrated its scalability beyond 100,000 MPI tasks, for molecular systems made of over 100,000 atoms.
Software: MGmol
- Authors: J.-L. Fattebert and D. Osei-Kuffuor
- O(N) First-Principles Molecular Dynamics
- ~95K lines C++
- Parallel: using MPI, scales beyond 100,000 CPUs
- Based on domain decomposition with nonoverlapping localized orbitals treated in parallel
Publications
- J.-L. Fattebert, J. Bernholc, Towards grid-based O(N) density-functional theory methods: optimized non-orthogonal orbitals and multigrid acceleration, Phys. Rev. B 62, no 3, 1713-1722 (2000).
- M. Buongiorno Nardelli, J.-L. Fattebert and J. Bernholc, O(N) real-space method for ab initio quantum transport calculations: Applications to carbon nanotube-metal contacts, Phys. Rev. B 64, 245423 (2001).
- F. Gygi, J.-L. Fattebert and E. Schwegler, Computation of Maximally Localized Wannier Functions using a Simultaneous Diagonalization Algorithm, Comput. Phys. Comm., 155, no 1 (2003), pp. 1-6.
- J.-L. Fattebert and F. Gygi, Linear scaling first-principles molecular dynamics with controlled accuracy, Comput. Phys. Comm., 162, no 1 (2004), pp. 24-36.
- J.-L. Fattebert and F. Gygi, Linear scaling first-principles molecular dynamics with plane-waves accuracy, Phys. Rev. B, 73, (2006), 115124.
- D. Osei-Kuffuor and J.-L. Fattebert, Accurate and Scalable O(N) Algorithm for First-Principles Molecular-Dynamics Computations on Large Parallel Computers, Phys. Rev. Lett. 112 (2014), 046401
- Daniel Osei-Kuffuor, Jean-Luc Fattebert, A Scalable O(N) Algorithm for Large-Scale Parallel First-Principles Molecular Dynamics Simulations, SIAM J. Scientific Computing 36(4) (2014)
Work performed under the auspices of the U. S. Department of Energy by Lawrence Livermore National Security, LLC under Contract DE-AC52-07NA27344. This is LLNL report UCRL-TR-228407.

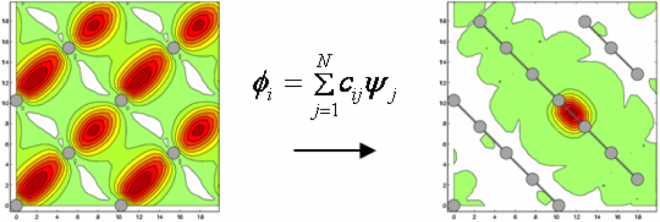
![Figure 5: comparing computer time for the standard Plane Waves approach (QBox code) and our linear scaling algorithm for a quantum simulation of liquid water (from Ref. [5])](/sites/default/files/styles/sidebar_2_up/public/figure4_0.png?itok=z9zrHQ8L)
![Figure 5: comparing computer time for the standard Plane Waves approach (QBox code) and our linear scaling algorithm for a quantum simulation of liquid water (from Ref. [5])](/sites/default/files/styles/sidebar_2_up/public/figure5.png?itok=2v9APU_m)